Passando para deixar, como prometido o exercício 5 do trabalho do 2 ano B, para fazer o download é só clicar no link que eu deixei. Caso tenham perguntas sobre a demonstração que eu deixei é só perguntar, no que se refere ao texto escrito acho que não tem nenhum problema, sobre as ilustrações aconselharia aos interessados que acrescentassem 1 desenho para cada uma das 3 etapas que descrevi na demonstração, uma vez que elas facilitam o entendimento do que está escrito. Divirtam-se!
sábado, 28 de abril de 2012
sexta-feira, 27 de abril de 2012
Charge do Dia
Nunca foi segredo para os alunos que eu gosto de tirinhas, ainda mais aquelas do Bill Watterson autor de Calvin and Hobbes, vendo algumas coisas minha resolvi postar algumas das tirinhas que vejo sobre escola, matemática e outras coisas começo essa seção com uma que me lembrou o trabalho de muitos alunos...
Explicando nossas origens...
 Muitos alunos já me perguntaram sobre o porque do nome do blog e sempre respondo que ele surgiu de uma brincadeira de alguns alunos que chamavam aos colegas que gostavam de exatas de ovelhas. Esta história sempre foi interessante e um tanto curiosa, sobretudo, porque nasceu da saudação Vulcana, algo muito nerd e relacionado com alunos que gostam de exatas já que a maioria acaba sendo rotulada assim...
Muitos alunos já me perguntaram sobre o porque do nome do blog e sempre respondo que ele surgiu de uma brincadeira de alguns alunos que chamavam aos colegas que gostavam de exatas de ovelhas. Esta história sempre foi interessante e um tanto curiosa, sobretudo, porque nasceu da saudação Vulcana, algo muito nerd e relacionado com alunos que gostam de exatas já que a maioria acaba sendo rotulada assim...Contudo, essa é apenas uma das razões... quando fala-se sobre a idéia de número não existe um autor para este conceito, mas o que sabe-se é que esta noção surgiu de situações vividas pelo homem. A História nos mostra que o homem inventou várias maneiras para realizar contagens e representá-las, e todas elas associadas ás necessidades de sua época. De forma geral o número sempre surge de uma associação básica que relaciona um objeto a outro, sendo uma das versões mais famosas a que fala sobre um pastor que quer contar seu rebanho de ovelhas.
Logo a matemática, assim como os números, sempre me lembra de ovelhas sendo essa uma das razões principais para o nome do blog ser homens e ovelhas. Isso é tudo!
quinta-feira, 26 de abril de 2012
Há mais ciência do que se parece em The Big Bang Theory
Quem é fã da série THE BIG BANG THEORY ao assistir o episódio 18 da 3ª temporada pode nem ter notado que havia um quadro branco em um dos cantos com um pouco de geometria não euclidiana. Por que ela estava
lá? E o que ela é?
 |
| O quadro branco do episódio referido |
Primeiro, lembremos que o próprio
Euclides desenvolveu sua geometria não-não-euclidiana em 300 A.C.. Ele começou
com a suposição do mínimo possível e deixou para gerações de alunos do Ensino
Fundamental a tarefa de provar todo o resto, que os triângulos têm 180 graus, e
daí por diante. Como é típico na matemática, o jogo envolve usar a menor quantidade
possível das mais elegantes postulações e deixar o resto às brilhantes
derivações.
Todo aluno do Ensino Fundamental aprende
os cinco axiomas de Euclides (brevemente listados, com a omissão de algumas
legalidades):
1. Quaisquer dois pontos podem ser ligados
por um segmento de reta.
2. Um segmento de reta pode ser estendido à
uma reta infinita.
3. Para qualquer segmento de reta, um
círculo pode ser desenhado.
4. Todos os ângulos retos são iguais.
Esses quatro parecem ser bem básicos. É
difícil imaginar que qualquer um deles possa ser comprovado ou refutado e, por
esse motivo, eles servem como pontos de partida óbvios. Mas Euclides adicionou
um enfadonho “quinto axioma”:
5. Para um ponto fora de uma reta, há
exatamente uma reta que passe pelo ponto que nunca fará intereseção com a reta
original.
Euclides era um cara esperto. Por que
simplesmente não provou o “quinto axioma” com os quatro primeiros? Ele tentou.
Durante 2.000 anos os matemáticos tentaram. Até mesmo Karl Friedrich Gauss. Sem
chance. Não foi provado. Os matemáticos modernos sabem que nunca poderia ser
provado com os quatro primeiros.
Então os matemáticos fizeram limões da
limonada. Em 1826, Nicolai Lobachevsky disse: “Vamos presumir que não há apenas
uma, e sim várias linhas paralelas como essa.”. Na década de 50 do século XIX,
Bernhard Riemann disse: “Vamos presumir que não há linha alguma.”. O caos
reinou. Sem o quinto axioma, nem mesmo podemos provar que todo triângulo tem
180 graus. Eis uma loucura maior ainda: adotar a versão do quinto axioma de
Lobachevsky faz com que os triângulos tenham menos de 180 graus. A versão de
Riemann faz com que tenham mais de 180. Mas que triângulos estranhos!
(Foi descoberto que tudo havia sido
resolvido décadas antes por Gauss, e que ele havia deixado a resolução em sua
mesa, sem nunca publicá-la. Um recado para os aspirantes a matemáticos:
qualquer que seja o projeto no qual estão trabalhando, há uma boa chance de
Gauss já tê-lo tentado antes.)
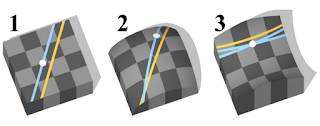 |
| 1. Geometria Euclidiana: existe uma reta paralela; 2. Geometria de Rieman: não existe retas paralelas; 3.Geometria de Lobachevsky: existem várias retas paralelas) |
Algumas décadas mais tarde, na virada do século XX, Albert Einstein e
alguns outros perceberam que há mais do que simples abstração no quinto axioma,
e ela estava relacionada a uma real incerteza que temos a respeito do nosso
próprio Universo. A incapacidade de provar o quinto axioma de Euclides é
equivalente a não saber se vivemos em um espaço curvo ou plano. Não sabemos ao
certo se triângulos extremamente grandes no nosso Universo têm exatamente 180
graus, ou então um pouco a mais ou a menos. Como é que um triângulo pode ter
mais de 180 graus? Façamos uma viagem:
 |
| É possível, ao andar pelo globo, fazer um triângulo com 3 ângulos retos. Este triângulo tem 270 graus, e não 180. |
Vamos andar (e andar de trenó e nadar também) desde o Polo Norte,
através do meridiano de Greenwich (longitude de 0 graus), passando pela
Inglaterra até chegarmos à Linha do Equador. Vire à direita. É um ângulo de 90
graus. Caminhe até chegar à ilha de São Salvador, ao leste do país Equador,
localizada na Linha do Equador no 90º meridiano (+90 graus). Agora vire
novamente à direita (são outros 90 graus) e volte para o norte, passando por
St. Louis, até o Polo Norte. Até agora, viramos duas vezes à direita, 90+90=180
graus. Mas aí chegamos ao Polo Norte novamente, atravessando o Canadá. Quando
chegamos, descobrimos que completamos um triângulo. Viramos três vezes. Mas
você está chegando em um ângulo reto em relação ao ponto de partida. O último
ângulo tem 90 graus. Então fizemos um triângulo com ângulos de 90+90+90= 270, e
não 180. Assim é a vida em um espaço curvado. Mesmo que você não enxergue a
curvatura enquanto caminha, ela está presente.
Você pode fazer o mesmo em um espaço de Lobachevsky. Imagine andar por
aí em cima de uma batata Pringles.
 |
| A geometria não euclidiana é elemento chave nas batatas Pringles |
 |
| De cima para baixo: plano esférico, plano hiperbólico e plano euclidiano. |
É frequente que um pedaço da abstração matemática possa ser observado
diretamente no nosso mundo físico. Nesse caso, nós apenas demoramos 2.000 anos
para perceber isso.
Em uma fascinante sequência de 1965 ao livro Flatland
(Planolândia), Dionys Burger relata em Sphereland
a vida do neto de Um Quadrado, chamado de Um Hexágono . Um pesquisador na
Planolândia fica consternado ao descobrir que a soma dos ângulos dos triângulos
não resulta em 180 graus. Um Hexágono, descendente do sagaz herói da
Planolândia, desperta seu amigo pesquisador para o fato de que os
planolandeses, na verdade, habitam um espaço curvo. Como aconteceu na nossa
viagem, a soma dos ângulos dos triângulos não resulta em 180 graus. (falarei melhor sobre esses livros depois, eles já apareceram em outro episódio da série The Big Bang Theory)
Até mesmo o nosso próprio espaço não-fictício e tridimensional pode ser
curvo. Nós apenas não sabemos disso. Os astrofísicos medem os maiores
triângulos que encontram e procuram pequenos desvios. Eles usam os raios da luz
mais antiga no universo, as microondas de apenas 380.000 anos após o Big Bang.
Até agora, todos os triângulos somaram 180 graus;no entanto, com um nível maior
de precisão, talvez possamos descobrir, a qualquer momento, que vivemos em um
espaço curvo. E isso não é problema. Só o que aconteceria é que todos os livros
de geometria do Ensino Fundamental teriam de revisar o quinto axioma de
Euclides. (É uma boa notícia para as editoras de livros escolares, que sempre
querem colocar uma nova edição à venda. Mesmo que não haja nada de novo, percebi
que, até mesmo nas minhas turmas, as editoras apenas mudam os números das
questões de 3 em 3 anos e chamam isso de uma nova edição.)
É divertido, mas o que isso tem a ver com a série? Por que colocamos
isso no quadro branco? Na verdade, é uma referência direta a uma fala que
Sheldon tinha no roteiro. Tinha. Era uma versão provisória do roteiro.
Os roteiros passam por muitas revisões ao longo da semana de produção.
Todos os dias os atores ensaiam e os escritores aprimoram o roteiro. A comédia
parece funcionar da mesma maneira que a ciência experimental. Às vezes os
roteiristas acham algo melhor. E nessa semana, após eu já ter enviado aos
cenógrafos as equações e os diagramas, os roteiristas reescreveram as falas de
Sheldon que tratavam do seu recolhimento ao espaço Riemanniano para relaxar.
Então os telespectadores nunca viram esse pedacinho da ciência. Os
roteiristas o substituíram com algo ainda mais engraçado: o espaço Riemannian
foi substituído pelo lugar preferido de Sheldon em Sim City. Mas talvez ainda
haja alguma relação. Afinal de contas, quem é que já mediu os triângulos de
Sheldonópolis?
Fonte : The Big Blog Theory
A conjectura de Goldbach
Uma conjectura matemática é uma proposição
(ideia) que muitos matemáticos acham que deve ser verdadeira, porém, ainda não
conseguiram prová-la. Você se lembra do que é um número primo? Um número maior
que 1 que só é divisível por 1 e por ele mesmo. São primos o 3, o 5, o 7. O 6
não é primo, pois é divisível por 3 e por 2.
A famosa Conjectura de Goldbach
diz que todo número par maior que 3 é igual a soma de dois
números primos. Por exemplo, 6 é igual a 3 + 3, 8 é igual a 3 +
5, 20 é igual a 7 + 13. Você pode ir verificando essa conjectura
para cada um dos números pares, um a um. Os matemáticos já verificaram para
milhares deles. Mas para que a conjectura vire um teorema é
preciso que alguém encontre uma prova que assegure que qualquer um dos infinitos números
pares pode ser escrito como soma de dois primos. A proposição é muito simples,
mas, até hoje, ninguém conseguiu demonstrá-la.
Por sinal o enunciado referente a conjectura de Goldbach é muito antigo. Em um epitáfio do Primeiro Cemitério de Atenas já encontra-se está
gravada a seguinte mensagem póstuma:
"Qualquer número par maior do
que 2 é a soma de dois números primos"
 |
| Carta de Goldbach para Euler |
Contundo, admiti-se, modernamente, que a
Conjectura de Goldbach foi enunciada pela primeira vez, em uma carta que Christian Goldbach enviou ao famoso matemático suíço Leonard Eüler no dia 7 de Julho de
1742, na qual ele observava que "qualquer número inteiro maior do que seis parecia ser a soma
de três números primos".
Foi Eüler que constatou que a afirmação feita por Goldbach se verdadeira, poderia ser decomposta em duas, como se admite atualmente: todo o número par, maior que dois, é a soma de dois primos; todo o número ímpar é a soma de três primos (Ironicamente, não foi Goldbach mas Eüler quem expressou a conjectura que tem o nome do primeiro).
Foi Eüler que constatou que a afirmação feita por Goldbach se verdadeira, poderia ser decomposta em duas, como se admite atualmente: todo o número par, maior que dois, é a soma de dois primos; todo o número ímpar é a soma de três primos (Ironicamente, não foi Goldbach mas Eüler quem expressou a conjectura que tem o nome do primeiro).
Destas duas afirmações, a segunda já foi provada para os ímpares suficientemente grandes por Vinogradov em meados dos anos 30, mas a primeira ainda não sendo justamente essa a que ficou conhecida hoje por conjectura de Goldbach, como já foi mencionado.É importante observar que quando Vinogradov usa o termo “suficientemente grande” ele quer dizer que todo número ímpar maior que certo número (o qual ele não define) tem a propriedade em questão. Isso significa que não sabemos a partir de que número a conclusão de Vinogradov vale, mas mesmo assim o resultado é muito importante, pois nos assegura que esta propriedade só não é válida para uma quantidade finita de números ímpares.
Esta conjectura é hoje considerada como um monstro da Teoria dos Números com mais de 200 anos na galeria dos resultados por demonstrar, tendo já inspirado muitos matemáticos. Para quem se interessar sobre o assunto um livro leve e interessante sobre o assunto é O Tio Petros e a Conjectura de Goldbach de Apostolos Doxiadis.
 |
| A capa do livro na edição brasileira |
O livro é escrito como um romance e tem como objetivo permitir perceber o
que é preciso para se fazer matemática, todo o prazer que está envolvido
nos momentos de contemplação mas também todas as dificuldades, e inclusivamente
perigos, que recheiam o caminho daqueles que se aventuram na criação
matemática, e claro fala um pouco sobre a Conjectura de Goldbach.
Estou deixando também uma versão do livro para download, porém está em espanhol...
O truque dos aniversários no mesmo dia
Continuando a brincar de mágico encontrei outro truque também envolve probabilidade. Se não tiver pelo
menos 50 pessoas na sala, este truque é um pouco arriscado. Mas qualquer coisa pode-se tentar um outro que resulta com elevada probabilidade desde que tenha umas 30
pessoas.
Diga que acaba de
adivinhar que há duas pessoas na sala que fazem aniversário no mesmo dia mas que não querem confirmar isso. Peça então a cada pessoa da platéia que escreva o dia e mês
do seu nascimento num papel e peça a uma outra para recolher e verificar as
datas. Verá que, com elevada probabilidade, há duas pessoas que comemoram aniversário no mesmo dia.
Mais uma vez é
surpreendente, mas as contas são fáceis de fazer. Esqueça os anos bissextos e
faça os cálculos com 356 dias. Depois, se o quiser, complique as contas
introduzindo o 29 de Fevereiro.
Qual a
probabilidade de duas pessoas apanhadas ao acaso terem nascido em dias
diferentes? É 364/365, claro. Fixa-se uma das pessoas e o seu dia de
aniversário e calcula-se a probabilidade de a segunda pessoa fazer anos em
qualquer dos restantes 364 dias do ano.
E qual será a
probabilidade de três pessoas fazerem anos em dias diferentes? Será a
probabilidade anterior vezes a probabilidade de a terceira pessoa fazer anos
num dos restantes 363 dias do ano, que é 363/365. Se fizer as contas verá que,
ao chegarmos à 23ª pessoa, o produto das probabilidades já é menor que 1/2.
Matemágica
 Para quem gosta de mágica aqui vai uma sugestão de truque capaz de surpreender a plateia. Este truque tem como base ideias matemáticas baseadas em probabilidade, porém o mágico tem de assumir algum risco quando faz estes turque. Mas isso
também torna o truque mais excitantes.
Para quem gosta de mágica aqui vai uma sugestão de truque capaz de surpreender a plateia. Este truque tem como base ideias matemáticas baseadas em probabilidade, porém o mágico tem de assumir algum risco quando faz estes turque. Mas isso
também torna o truque mais excitantes.
Imagine o você que tem um público de umas dezenas de pessoas. Comece por recordar com elas que os
números das portas de suas casas têm um primeiro dígito significativo e que esse
dígito é 1, 2, 3, 4, 5, 6, 7, 8 ou 9. Lembre que um número de porta não pode começar por
zero.
Em seguida, confirme que as pessoas moram em ruas diferentes e que não escolheram o número
da sua porta, logo tem-se que o primeiro dígito significativo de cada número é
aleatório. Sendo assim, e havendo muitas pessoas , é natural se pensar que possa a
haver tantos números de porta começando com o número 1, quanto com o número 2, como por qualquer outro dos 9 dígitos possíveis. Mas se você pensar um pouco conseguirá descobrir que não é assim e que há mais pessoas com número de
porta começando por 1, 2, 3 ou 4 do que começando por 5, 6, 7, 8 ou 9. No
primeiro caso temos quatro hipóteses e no segundo cinco, pelo que deveria ser o
contrário, pensará o público.
Peça agora para as
pessoas no primeiro caso levantarem os braços. Peça depois para as pessoas no
segundo grupo fazerem o mesmo.
Habitualmente, não
vale a pena contar os braços. A aposta vence-se com grande margem. Se não
quiser arriscar, não aposte. Mas se estiver bem-disposto, aposte que há
mais pessoas com número de porta começando por 1, 2 ou 3 do que começando por
qualquer um dos restantes seis dígitos. Nesta segunda aposta parece que tem
dois terços de probabilidade de perder, mas, na realidade, é mais provável que
volte a ganhar do que perder.
As magias
matemáticas não têm piada quando não se explicam. O que acontece é que, para
qualquer dos nove dígitos ter a mesma probabilidade de ocorrência, cada rua
teria de ter exatamente 9 portas, ou 99, ou 999...
É fácil: se uma
rua tiver portas numeradas de 1 a 9, qualquer algarismo tem 1/9 de
probabilidade de aparecer. O mesmo se passa se a rua tiver 99 portas, e assim
por diante. Mas as ruas não costumam ter essa dimensão exata.
Imagine uma rua
com 33 portas. O dígito 1 aparece como primeiro algarismo significativo 11
vezes, pois aparece nas portas 1, 10, 11, 12, 13, 14, 15, 16, 17, 18 e 19. O
dígito 2 aparece também 11 vezes a liderar o número das portas. O 3 já só
aparece cinco, enquanto o 4 e todos os restantes aparecem apenas uma vez. Pegue
em papel e lápis, que são os instrumentos preferidos dos matemáticos, e
verifique.
O que se passa com
os números das portas da rua passa-se com muitos outros, desde as cotações das
ações e dos índices de inflação até constantes físicas e matemáticas. Quem o
descobriu foi o astrónomo norte-americano Simon Newcomb, em 1881, mas quem o
estudou de forma sistemática foi um seu conterrâneo, o físico Frank Benford, em
1938. Por isso, a lei de distribuição dos primeiros dígitos significativos
chama-se hoje Lei de Benford
Assinar:
Postagens (Atom)






