Quem é fã da série THE BIG BANG THEORY ao assistir o episódio 18 da 3ª temporada pode nem ter notado que havia um quadro branco em um dos cantos com um pouco de geometria não euclidiana. Por que ela estava
lá? E o que ela é?
 |
| O quadro branco do episódio referido |
Primeiro, lembremos que o próprio
Euclides desenvolveu sua geometria não-não-euclidiana em 300 A.C.. Ele começou
com a suposição do mínimo possível e deixou para gerações de alunos do Ensino
Fundamental a tarefa de provar todo o resto, que os triângulos têm 180 graus, e
daí por diante. Como é típico na matemática, o jogo envolve usar a menor quantidade
possível das mais elegantes postulações e deixar o resto às brilhantes
derivações.
Todo aluno do Ensino Fundamental aprende
os cinco axiomas de Euclides (brevemente listados, com a omissão de algumas
legalidades):
1. Quaisquer dois pontos podem ser ligados
por um segmento de reta.
2. Um segmento de reta pode ser estendido à
uma reta infinita.
3. Para qualquer segmento de reta, um
círculo pode ser desenhado.
4. Todos os ângulos retos são iguais.
Esses quatro parecem ser bem básicos. É
difícil imaginar que qualquer um deles possa ser comprovado ou refutado e, por
esse motivo, eles servem como pontos de partida óbvios. Mas Euclides adicionou
um enfadonho “quinto axioma”:
5. Para um ponto fora de uma reta, há
exatamente uma reta que passe pelo ponto que nunca fará intereseção com a reta
original.
Euclides era um cara esperto. Por que
simplesmente não provou o “quinto axioma” com os quatro primeiros? Ele tentou.
Durante 2.000 anos os matemáticos tentaram. Até mesmo Karl Friedrich Gauss. Sem
chance. Não foi provado. Os matemáticos modernos sabem que nunca poderia ser
provado com os quatro primeiros.
Então os matemáticos fizeram limões da
limonada. Em 1826, Nicolai Lobachevsky disse: “Vamos presumir que não há apenas
uma, e sim várias linhas paralelas como essa.”. Na década de 50 do século XIX,
Bernhard Riemann disse: “Vamos presumir que não há linha alguma.”. O caos
reinou. Sem o quinto axioma, nem mesmo podemos provar que todo triângulo tem
180 graus. Eis uma loucura maior ainda: adotar a versão do quinto axioma de
Lobachevsky faz com que os triângulos tenham menos de 180 graus. A versão de
Riemann faz com que tenham mais de 180. Mas que triângulos estranhos!
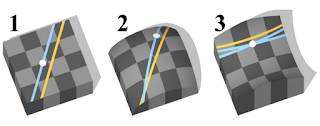 |
| 1. Geometria Euclidiana: existe uma reta paralela; 2. Geometria de Rieman: não existe retas paralelas; 3.Geometria de Lobachevsky: existem várias retas paralelas) |
(Foi descoberto que tudo havia sido
resolvido décadas antes por Gauss, e que ele havia deixado a resolução em sua
mesa, sem nunca publicá-la. Um recado para os aspirantes a matemáticos:
qualquer que seja o projeto no qual estão trabalhando, há uma boa chance de
Gauss já tê-lo tentado antes.)
Algumas décadas mais tarde, na virada do século XX, Albert Einstein e
alguns outros perceberam que há mais do que simples abstração no quinto axioma,
e ela estava relacionada a uma real incerteza que temos a respeito do nosso
próprio Universo. A incapacidade de provar o quinto axioma de Euclides é
equivalente a não saber se vivemos em um espaço curvo ou plano. Não sabemos ao
certo se triângulos extremamente grandes no nosso Universo têm exatamente 180
graus, ou então um pouco a mais ou a menos. Como é que um triângulo pode ter
mais de 180 graus? Façamos uma viagem:
 |
| É possível, ao andar pelo globo, fazer um triângulo com 3 ângulos retos. Este triângulo tem 270 graus, e não 180. |
 |
| Observe que uma esfera é dita um espaço não euclidiano, entretanto localmente as leis da geometria euclidiana são boas aproximações. Em um pequeno triângulo na face da Terra a soma dos internos é aproximadamente 180graus. |
Vamos andar (e andar de trenó e nadar também) desde o Polo Norte,
através do meridiano de Greenwich (longitude de 0 graus), passando pela
Inglaterra até chegarmos à Linha do Equador. Vire à direita. É um ângulo de 90
graus. Caminhe até chegar à ilha de São Salvador, ao leste do país Equador,
localizada na Linha do Equador no 90º meridiano (+90 graus). Agora vire
novamente à direita (são outros 90 graus) e volte para o norte, passando por
St. Louis, até o Polo Norte. Até agora, viramos duas vezes à direita, 90+90=180
graus. Mas aí chegamos ao Polo Norte novamente, atravessando o Canadá. Quando
chegamos, descobrimos que completamos um triângulo. Viramos três vezes. Mas
você está chegando em um ângulo reto em relação ao ponto de partida. O último
ângulo tem 90 graus. Então fizemos um triângulo com ângulos de 90+90+90= 270, e
não 180. Assim é a vida em um espaço curvado. Mesmo que você não enxergue a
curvatura enquanto caminha, ela está presente.
Você pode fazer o mesmo em um espaço de Lobachevsky. Imagine andar por
aí em cima de uma batata Pringles.
 |
| A geometria não euclidiana é elemento chave nas batatas Pringles |
 |
| De cima para baixo: plano esférico, plano hiperbólico e plano euclidiano. |
É frequente que um pedaço da abstração matemática possa ser observado
diretamente no nosso mundo físico. Nesse caso, nós apenas demoramos 2.000 anos
para perceber isso.
Em uma fascinante sequência de 1965 ao livro Flatland
(Planolândia), Dionys Burger relata em Sphereland
a vida do neto de Um Quadrado, chamado de Um Hexágono . Um pesquisador na
Planolândia fica consternado ao descobrir que a soma dos ângulos dos triângulos
não resulta em 180 graus. Um Hexágono, descendente do sagaz herói da
Planolândia, desperta seu amigo pesquisador para o fato de que os
planolandeses, na verdade, habitam um espaço curvo. Como aconteceu na nossa
viagem, a soma dos ângulos dos triângulos não resulta em 180 graus. (falarei melhor sobre esses livros depois, eles já apareceram em outro episódio da série The Big Bang Theory)
Até mesmo o nosso próprio espaço não-fictício e tridimensional pode ser
curvo. Nós apenas não sabemos disso. Os astrofísicos medem os maiores
triângulos que encontram e procuram pequenos desvios. Eles usam os raios da luz
mais antiga no universo, as microondas de apenas 380.000 anos após o Big Bang.
Até agora, todos os triângulos somaram 180 graus;no entanto, com um nível maior
de precisão, talvez possamos descobrir, a qualquer momento, que vivemos em um
espaço curvo. E isso não é problema. Só o que aconteceria é que todos os livros
de geometria do Ensino Fundamental teriam de revisar o quinto axioma de
Euclides. (É uma boa notícia para as editoras de livros escolares, que sempre
querem colocar uma nova edição à venda. Mesmo que não haja nada de novo, percebi
que, até mesmo nas minhas turmas, as editoras apenas mudam os números das
questões de 3 em 3 anos e chamam isso de uma nova edição.)
É divertido, mas o que isso tem a ver com a série? Por que colocamos
isso no quadro branco? Na verdade, é uma referência direta a uma fala que
Sheldon tinha no roteiro. Tinha. Era uma versão provisória do roteiro.
Os roteiros passam por muitas revisões ao longo da semana de produção.
Todos os dias os atores ensaiam e os escritores aprimoram o roteiro. A comédia
parece funcionar da mesma maneira que a ciência experimental. Às vezes os
roteiristas acham algo melhor. E nessa semana, após eu já ter enviado aos
cenógrafos as equações e os diagramas, os roteiristas reescreveram as falas de
Sheldon que tratavam do seu recolhimento ao espaço Riemanniano para relaxar.
Então os telespectadores nunca viram esse pedacinho da ciência. Os
roteiristas o substituíram com algo ainda mais engraçado: o espaço Riemannian
foi substituído pelo lugar preferido de Sheldon em Sim City. Mas talvez ainda
haja alguma relação. Afinal de contas, quem é que já mediu os triângulos de
Sheldonópolis?





































